At the end of this blog post, you should be able to understand how to;
- solve problems involving resistivity and conductivity
- deduce the equivalent resistance of series and parallel circuits
- solve problems on series and parallel resistors
Example: A cylinder wire of 1.5m in length, 5.0mm in diameter, has a resistance of 3.5Ohms. Calculate the resistivity of the wire.
formula, R = 𝔓L/A
Solution
Length, L = 1.5m, 𝔓= resistivity = ?
Radius r = 5.0mm/2 = 2.5mm = 2.5×10⁻³m
Cross sectional area, A = πr² = 22/7 × (2.5×10⁻³)²m²
𝔓= RA/L = [3.5 × (22/7) × (2.5 ×10⁻³)² ] ÷ 0.5
𝔓= 45.833 × 10⁻⁶ ohm-meter
A wire of diameter 0.6mm, resistivity 1.1 × 10⁻⁶Ωm has resistance of 44Ω. Calculate the length of the wire.
Soution
Here, we are given:
Radius, r = 0.6/2 mm = 3 × 10⁻⁴m
To find L we deduce it from 𝔓= RA/L (i.e L = RA/𝔓)
L = [ 44 × 22/7 × (3 × 10⁻⁴)² ] ÷ 1.1 10⁻⁶
L = 11.3m
Here, we are given:
Radius, r = 0.6/2 mm = 3 × 10⁻⁴m
To find L we deduce it from 𝔓= RA/L (i.e L = RA/𝔓)
L = [ 44 × 22/7 × (3 × 10⁻⁴)² ] ÷ 1.1 10⁻⁶
L = 11.3m
A 30m conductor of cross sectional area 2mm has a resistance of 10Ω. Calculate the conductivity of the conductor.
Solution
𝔓= L/RA
= 30 ÷ [10 × 2(10⁻³)² = 1.5 × 10⁶ (Ωm)⁻¹
𝔓= L/RA
= 30 ÷ [10 × 2(10⁻³)² = 1.5 × 10⁶ (Ωm)⁻¹
EQUIVALENT RESISTANCE OF SERIES AND PARALLEL CIRCUIT
Equivalent Resistance of a series circuit
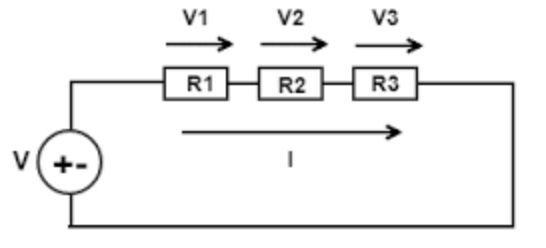
- When resistors of resistance R₁, R₂ and R₃ are joint together, they’re said to be connected in series. It should be noted that;
The current through a series circuit is the same all over ( I.e I=i₁=i₂=i₃).
The voltage drop across each resistor is different depending on its resistances
The applied voltage (Vs) is equal to the sum of the Potential difference across each resistor. (i.e Vs = V(R₁) + V(R₂) + V(R₃) or V = V₁ + V₂ + V₃
Where Vs = IR; V₁ = IR₁; V₂ = IR₂; V₃ = IR₃
IR = IR₁ + IR₂ + IR₃
⇒(equivalent resistance), Req = R₁ + R₂ + R₃
For n resistors connected in series, the equivalent resistance
Req is given by Req = R₁ + R₂ + R₃+ ……..Rₙ
EQUIVALENT RESISTANCE OF A PARALLEL CIRCUIT
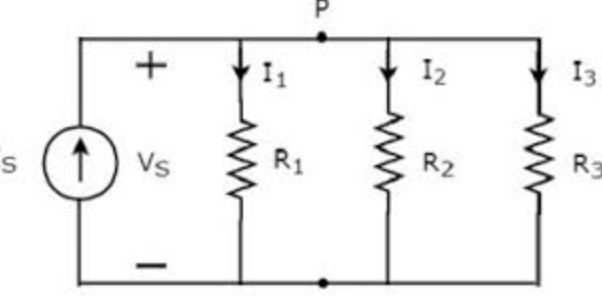
When sistors of resistance R₁, R₂ and R₃ are connected in parallel, the following statements hold good;
The p.d across each resistor is the same
The current flowing through each resistor is different
The supply current (I) is equal to the sum of current flowing through each resistor i.e Vs = V₁ = V₂ = V₃
I = i₁ + i₂ + i₃
Where I = Vs/R; i₁ = Vs/R₁; i₂ = Vs/R₂; i₃ = Vs/R₃
Recall I = Vs/R
Therefore, Vs/R = Vs/R₁ + Vs/R₂ + Vs/R₃
⇒1/R = 1/Req = 1/R₁ + 1/R₂ + 1/R₃
For n resistors connected in parallel
1/Req = 1/R₁ + 1/R₂ + 1/R₃…….+ 1/Rₙ
The p.d across each resistor is the same
The current flowing through each resistor is different
The supply current (I) is equal to the sum of current flowing through each resistor i.e Vs = V₁ = V₂ = V₃
I = i₁ + i₂ + i₃
Where I = Vs/R; i₁ = Vs/R₁; i₂ = Vs/R₂; i₃ = Vs/R₃
Recall I = Vs/R
Therefore, Vs/R = Vs/R₁ + Vs/R₂ + Vs/R₃
⇒1/R = 1/Req = 1/R₁ + 1/R₂ + 1/R₃
For n resistors connected in parallel
1/Req = 1/R₁ + 1/R₂ + 1/R₃…….+ 1/Rₙ
Example: In the circuit below, determine the two voltages drops across R₁ and R₂?
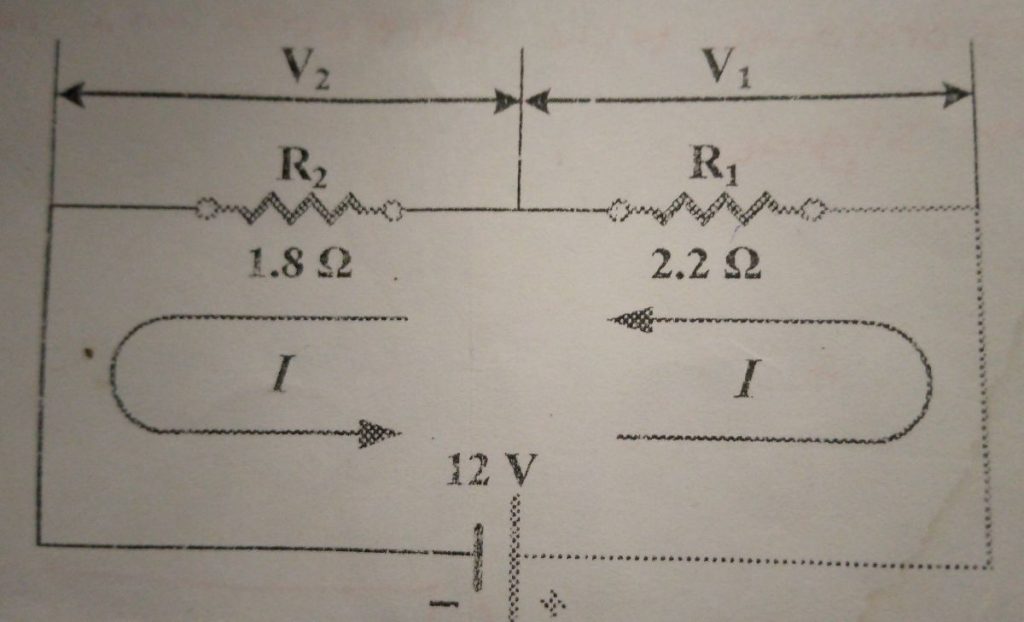
Solution
R₁ = 2.2Ω, R₂ = 1.8Ω, V = 12v, I = ?, V₁ = ?, V₂ = ?
First solve for total resistance
RT = R₁ + R₂
= 2.2 + 1.8 = 4Ω
Second, solve for current:
I = V/RT = 12/4 = 3 amp
Finally, solve for voltage drop across any resistor
Voltage drop across R
V₁ = I × R₁ = 3 × 2.2 = 6.6v
Voltage drop across R
V₂ = I × R₂ = 3 × 1.8 = 5.4v
The sum of all voltage drops (6.6v + 5.4v) equals the source voltage (12v).
R₁ = 2.2Ω, R₂ = 1.8Ω, V = 12v, I = ?, V₁ = ?, V₂ = ?
First solve for total resistance
RT = R₁ + R₂
= 2.2 + 1.8 = 4Ω
Second, solve for current:
I = V/RT = 12/4 = 3 amp
Finally, solve for voltage drop across any resistor
Voltage drop across R
V₁ = I × R₁ = 3 × 2.2 = 6.6v
Voltage drop across R
V₂ = I × R₂ = 3 × 1.8 = 5.4v
The sum of all voltage drops (6.6v + 5.4v) equals the source voltage (12v).
