SIGNALS
Signals is a physical quantity or an electrical waveform that carries information. It can also be define as a pattern, or changes that convey information from a source to a destination. The purpose of a signal is to transmit this information timely and accurately.
In the context of communication systems, a signal is a physical quantity or an electrical waveform that carries information. It can be any variation or disturbance that can be measured or observed and represents meaningful data or instructions.
A signal contains patterns, patterns, or changes that convey information from a source to a destination. The information can be in the form of voice, video, data, or any other type of content. The purpose of a signal is to transmit this information reliably and accurately.
Signals can take different forms depending on the type of communication system. They can be analog or digital. Analog signals are continuous waveforms that vary in time and amplitude, while digital signals are discrete and represent information using a series of discrete values, typically binary digits (bits) 0 and 1.
Signals are characterized by various parameters, such as amplitude, frequency, phase, and duration. These parameters define the characteristics of the signal and influence how it is transmitted, received, and processed.
In communication systems, signals are generated by a source, modulated or encoded to fit the transmission medium, transmitted through a channel, received by a destination, and finally decoded or demodulated to extract the original information.
Overall, a signal is a physical or electrical representation of information that is used to transmit data in various communication systems. It is a fundamental concept in understanding how information is conveyed from one point to another.
In digital communications, signals play a crucial role in transmitting information from one point to another. Signals can be broadly classified into two types: analog signals and digital signals. Each type of signal has its own characteristics and is used in different applications.
1. Analog Signals:
Analog signals are continuous waveforms that vary in time and amplitude. They can take any value within a defined range, and their values correspond to the variations in the original information being transmitted. Examples of analog signals include audio signals, voltage signals, and electromagnetic waves.
Analog signals are commonly used in traditional communication systems such as analog telephony, AM/FM radio, and television broadcasting. However, they are susceptible to noise and distortion during transmission, which can degrade the quality of the received signal.
2. Digital Signals:
Digital signals, on the other hand, are discrete and represent information using a series of discrete values, typically binary digits (bits) 0 and 1. Digital signals are more robust against noise and interference compared to analog signals. They can be accurately reproduced, making them ideal for long-distance and high-speed data transmission.
Digital signals are widely used in modern communication systems such as the internet, mobile networks, and computer networks. In these systems, digital information is encoded into binary form and transmitted as a sequence of 0s and 1s. Various modulation techniques, such as amplitude shift keying (ASK), frequency shift keying (FSK), and phase shift keying (PSK), are employed to convert digital signals into analog waveforms for transmission over physical media like cables or wireless channels.
Advantages of Digital Signals:
– Immunity to noise: Digital signals can be received with minimal errors even in the presence of noise, provided the noise level is below a certain threshold.
– Better signal quality: Digital signals can be regenerated and restored to their original form without degradation, allowing for error detection and correction techniques.
– Efficient use of bandwidth: Digital signals can be compressed and multiplexed, enabling efficient utilization of available bandwidth.
In summary, signals in digital communications can be categorized as analog signals and digital signals. Analog signals are continuous waveforms, while digital signals are discrete representations of information. Digital signals provide several advantages over analog signals, including noise immunity, improved signal quality, and efficient bandwidth utilization, making them the preferred choice for modern communication systems.
Properties of Signals
Signals possess several properties that are essential to understand their behavior and characteristics. Here are some important properties of signals:
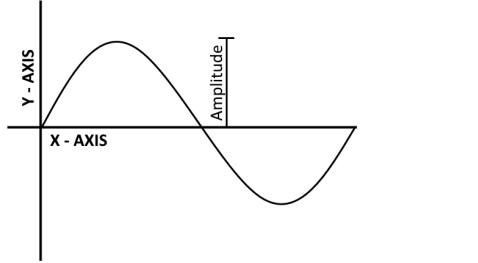
- Amplitude: The amplitude of a signal refers to the magnitude or strength of the signal. It represents the maximum displacement from the baseline or the zero reference level. In analog signals, the amplitude corresponds to the intensity or voltage level of the waveform. In digital signals, the amplitude represents discrete levels, typically represented by binary digits (0s and 1s).
- Frequency: Frequency refers to the number of cycles or oscillations that occur within a given time period. It is measured in Hertz (Hz). In analog signals, frequency determines the pitch of the waveform, while in digital signals, it represents the rate at which signal transitions occur.
- Phase: Phase refers to the relative position or timing of a signal waveform with respect to a reference. It is typically measured in degrees or radians. Phase is crucial in determining how signals interact with each other, especially in applications like modulation and interference.
- Duration: Duration represents the length of time that a signal persists or exists. It is an important property in analyzing signal transmission and reception. Signals can be categorized as transient (short-duration) or continuous (long-duration) based on their duration.
- Periodicity: Periodicity refers to whether a signal exhibits a repetitive pattern or not. Periodic signals repeat the same pattern over regular intervals. Sinusoidal waveforms are examples of periodic signals. Non-periodic signals, also known as aperiodic signals, do not repeat their pattern over time.
- Symmetry: Symmetry describes the balance or distribution of a signal waveform. A signal can exhibit symmetry about the vertical axis (even symmetry) or about the horizontal axis (odd symmetry). Symmetry can affect signal processing and modulation techniques.
- Bandwidth: Bandwidth refers to the range of frequencies that a signal occupies or occupies for transmission. It represents the ability of a signal to carry information. In analog signals, bandwidth determines the frequency range over which the signal is transmitted. In digital signals, bandwidth represents the maximum data rate that can be transmitted over a channel.
- Energy and Power: Energy and power are measures of the total or average amount of signal energy over time. Energy is related to the finite duration of a signal, while power is the energy per unit time. These properties are important in signal analysis, as they provide insights into the signal’s characteristics and requirements for transmission and reception.
Understanding the properties of signals is fundamental in signal processing, modulation, demodulation, filtering, and various other aspects of communication systems. By analyzing and manipulating these properties, engineers can design efficient and reliable communication systems to transmit and receive information accurately.
Fourier Series Analysis
Fourier series is a mathematical representation that allows us to decompose periodic signals into a sum of sinusoidal components. It provides a way to analyze and understand the frequency content of a signal. The Fourier series representation of a periodic signal is given by:
f(t) = A0 + Σ [Ancos(nω0t) + Bnsin(nω0t)]
In this equation, f(t) represents the periodic signal, ω0 is the fundamental angular frequency (2π/T), where T is the period of the signal, An and Bn are the Fourier coefficients that determine the amplitude of each sinusoidal component, and A0 is the DC component or the average value of the signal.
The coefficients An and Bn can be calculated using the following formulas:
An = (2/T) * ∫[f(t) * cos(nω0t)] dt
Bn = (2/T) * ∫[f(t) * sin(nω0t)] dt
The integration is performed over one period of the signal.
The Fourier series allows us to represent a wide range of periodic signals, including square waves, triangular waves, sawtooth waves, and more, as a sum of sinusoidal components. By determining the Fourier coefficients, we can understand the contribution of each frequency component to the overall signal.
The Fourier series has several important properties:
- Linearity: The Fourier series is linear, meaning that if a signal can be represented by f1(t) and another signal by f2(t), then a linear combination of these signals can be represented by a linear combination of their respective Fourier series.
- Parseval’s Theorem: Parseval’s theorem states that the total power of a signal is equal to the sum of the powers of its frequency components. Mathematically, it is expressed as the integral of the squared magnitude of the signal being equal to the sum of the squared magnitudes of its Fourier coefficients.
- Convergence: The Fourier series converges to the original periodic signal as the number of terms in the series approaches infinity. This property allows us to approximate a periodic signal using a finite number of terms while still capturing its essential characteristics.
The Fourier series has a wide range of applications in various fields, including signal processing, communications, image processing, and audio/video compression. It provides a powerful tool for analyzing and manipulating periodic signals by revealing their frequency components and aiding in the design of filters, modulation schemes, and other signal processing techniques.
To analyze a signal using Fourier series equations, you need to follow these steps:
1. Determine the Period: Identify the period of the signal you want to analyze. The period is the time it takes for the signal to complete one full cycle.
2. Express the Signal as a Periodic Function: If the signal is not already periodic, extend it periodically by repeating the signal over its period. This step assumes that the signal repeats itself indefinitely.
3. Calculate the DC Component (A0): Find the average value of the periodic signal over one period. This represents the DC component of the signal.
4. Calculate the Fourier Coefficients (An and Bn): Use the following formulas to calculate the coefficients:
An = (2/T) * ∫[f(t) * cos(nω0t)] dt
Bn = (2/T) * ∫[f(t) * sin(nω0t)] dt
Here, f(t) is the periodic signal, and ω0 is the fundamental angular frequency (2π/T), where T is the period of the signal.
Perform the integrations over one period of the signal. These coefficients represent the amplitudes of the cosine and sine components at each frequency.
5. Determine the Frequency Components: The frequency components of the signal are given by the multiples of the fundamental frequency (ω0). The higher the value of n, the higher the frequency component.
The magnitude of the coefficients An and Bn represents the amplitude of each frequency component, while the phase angle determines the phase shift of each component.
6. Construct the Fourier Series Representation: Write the Fourier series equation using the calculated coefficients:
f(t) = A0 + Σ [An*cos(nω0t) + Bn*sin(nω0t)]
Include the DC component (A0) and the cosine and sine components for each frequency.
7. Visualization and Interpretation: Plot the Fourier series representation to visualize the signal’s frequency components. The plot will show the contribution of each frequency component to the overall signal.
By following these steps, you can analyze a signal using Fourier series equations and gain insights into its frequency content and composition. This analysis is useful for understanding the signal’s behavior, identifying dominant frequencies, and performing various signal processing tasks, such as filtering, modulation, and compression.
