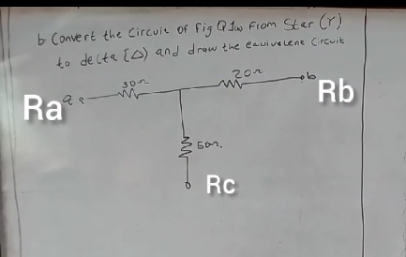
First of all, you need to understand how star and delta looks like. There are two different popular ways star and delta, could be provided to you.
Diagram

Where Ra = 30Ω, Rb = 20Ω and Rc = 50Ω
The star network three branches are represented by Ra, Rb and Rc
The delta network three branches are represented by R1, R2 and R3
So to find delta, we’ve to look for R1, R2 and R3
R1 = [RaRb + RbRc + RcRa]/Rb
= ( 30×20 + 20×50 + 50×30 )/20
= ( 600 + 1000 + 1500 )/20
= (3100 ÷ 20)
= 155Ω
R2 = [RaRb + RbRc + RcRa]/Rc
= ( 30×20 + 20×50 + 50×30 )/50
= ( 600 + 1000 + 1500 )/50
= (3100 ÷ 50)
= 62Ω
R3 = [RaRb + RbRc + RcRa]/Ra
= ( 30×20 + 20×50 + 50×30 )/30
= ( 600 + 1000 + 1500 )/30
= (3100 ÷ 30)
= 103.3Ω
Now, R1= 155Ω, R2 = 62Ω, R3 = 103.33Ω
Redraw the circuit, to delta conversion

How to convert from delta to star
We’ve to look for Ra, Rb and Rc
Recall, R1= 155Ω, R2 = 62Ω, R3 = 103.33Ω
Ra = (R1×R2 ) ÷ (R1 + R2 + R3)
= (155×62) ÷ ( 155+62+103.3)
= 9610 ÷ 320
= 30Ω
Rb = (R2×R3 ) ÷ (R1 + R2 + R3)
= (62×103.3) ÷ ( 155+62+103.3)
= 6386 ÷ 320
= 20Ω
Rc = (R1×R3 ) ÷ (R1 + R2 + R3)
= (155×103.3) ÷ ( 155+62+103.3)
= 15965 ÷ 320
= 50Ω
Now, R1= 155Ω, R2 = 62Ω, R3 = 103.33Ω
you can see it gave us the same value for star conversion
Redraw the circuit, to star conversion