Determine the frequency of an oscillator given the inductance and capacitance, if the capacitor varied between 20pF-150pF | Electrical Engineering Questions

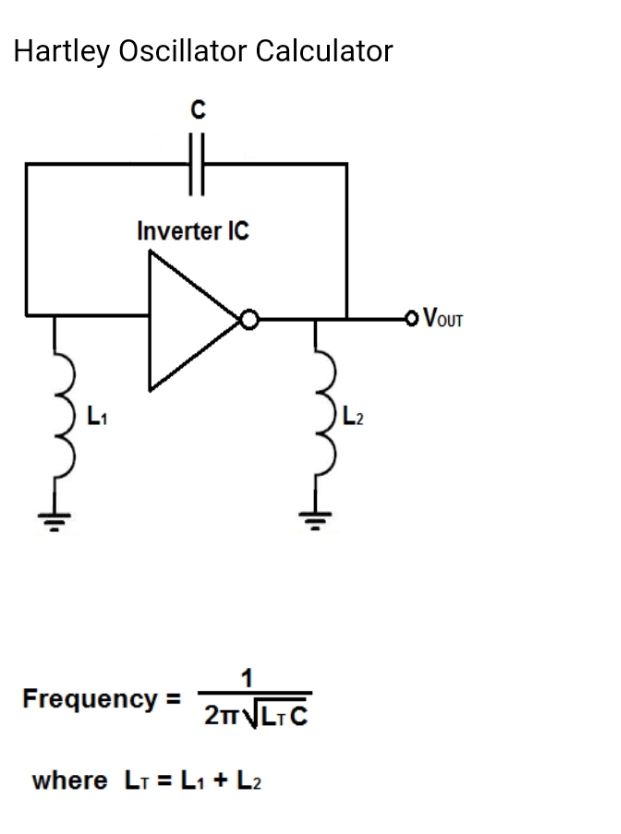
1. A frequency determining circuit in an L-C sinewave oscillator consist of a high Q inductance L = 200μH in parallel with a capacitor of C = 450pF. Determine the frequency range of the oscillator if this capacitor, can be varied between 20pF-150pF.

Solution
Inductance, L = 200μH
= 200 × 10–⁶H
Capacitance, C = 450pF
= 450 × 10–¹²F.
LC = Inductance × Capacitance
200 × 10–⁶H × 450 × 10–¹²F = 9 × 10–¹⁴
Find the root of LC, √(LC) = 3 × 10–⁷

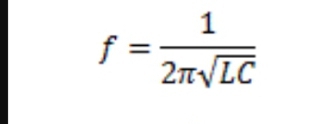
Therefore fo = 1/[2π√(LC)] = 1/[2π × 3 × 10–⁷]= 1/[2 × 3.142 × 3 × 10–⁷]= 1/0.0000018852
= 530447.7Hz
Approximately, = 530.4KHz

Continuation
When the variable capacitor C1 is connected in parallel with the circuit, the total capacitance in parallel with the inductor is increased to C+ C1, thus the corresponding oscillator frequency changes to

2. The resonant circuit of a tuned-collector oscillator has a resonant frequency of 5MHz if the value of the capacitance is increased by 50%. Calculate the new resonant frequency.

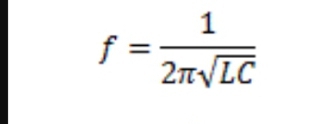
SOLUTION
f_o= 1/[2π√(LC)] Hz ………………………….. (1)
5 × 10⁶ = fo = 1/2π√LC ………………………. (2)
fo = 1/2π√L×1.5C …………………………….. (3)
Divide equation (3) by equation (2)
f_o/5×10⁶, = 1/√1.5 or f_o= 4.08MHz

3. A certain X-cut Quartz crystal resonate at 450KHz. It has an equivalent inductance of 4.2H and an equivalent capacitance of 0.0297pF. If its equivalent resistance to 600ohms, calculate Q factor.

Solution
Q = wL/R =( wavelength × Length, L)/resistance
Wavelength = 2πF
Q = 2πFL/R = (2×3.142×450,000×4.2)/600
11,876,760/600 = 19,794.6

4. A tuned-collector oscillator has fixed inductance of 100μH and has to be tuneable over the frequency band of 500KHz to 1500KHz. Find the range of the variable capacitor to be used.

Solution
Parameters given, inductance,L = 100μF ;= 100×10–⁶F

Frequency band = 500KHz – 1500KHz

Resonant frequency is given by;

f_o=(oscillator frequency) = 1÷2π√(LC) or 1/2π√(LC)

C = 1 ÷ 4π2f02L or 1/4π2f02L

Where L and C refer to the tuned circuit, therefore when f_o= 500KHz

C = 1/4π2 × (500 × 10³)² × 100 × 10–⁶

= 1015pF

f_o= 500KHz

C = 1/4π2 × (1500 × 10³)² × 100 × 10–⁶

= 113pF

The range of the variable capacitor to be used is = 113 – 1015pF